
There are drugs, called enantiopure drugs, that have different effects based on whether the drug is a racemic mixture or purely one enantiomer. Optical isomers have basically the same properties (melting points, boiling points, etc.) but there are a few exceptions (uses in biological mechanisms and optical activity). Optical isomers also have no axis of symmetry, which means that there is no line that bisects the compound such that the left half is a mirror image of the right half. Our left hand is a mirror image of our right, yet there is no way our left thumb can be over our right thumb if our palms are facing the same way and placed over one another. Two enantiomers are nonsuperimposible mirror images of one another (i.e., chiral), with the most common cited example being our hands. L.C.Optical isomers, or enantiomers, have the same sequence of atoms and bonds but are different in their 3D shape. Word problems on sum of the angles of a triangle is 180 degreeĭomain and range of rational functions with holesĬonverting repeating decimals in to fractionsĭecimal representation of rational numbers Word problems on direct variation and inverse variationĬomplementary and supplementary angles word problems Sum of the angle in a triangle is 180 degreeĭifferent forms equations of straight lines Trigonometric ratios of supplementary anglesĭomain and range of trigonometric functionsĭomain and range of inverse trigonometric functions Trigonometric ratios of complementary angles Trigonometric ratios of angles greater than or equal to 360 degree
#COUNTER CLOCKWISE ROTATION FORMULA PLUS#
Trigonometric ratios of 270 degree plus theta Trigonometric ratios of 270 degree minus theta Trigonometric ratios of 180 degree minus theta Trigonometric ratios of 180 degree plus theta Trigonometric ratios of 90 degree plus theta Trigonometric ratios of 90 degree minus theta Trigonometric ratios of some negative angles Trigonometric ratios of some specific angles Nature of the roots of a quadratic equation worksheetsĭetermine if the relationship is proportional worksheet Writing and evaluating expressions worksheet Quadratic equations word problems worksheetĭistributive property of multiplication worksheet - Iĭistributive property of multiplication worksheet - II

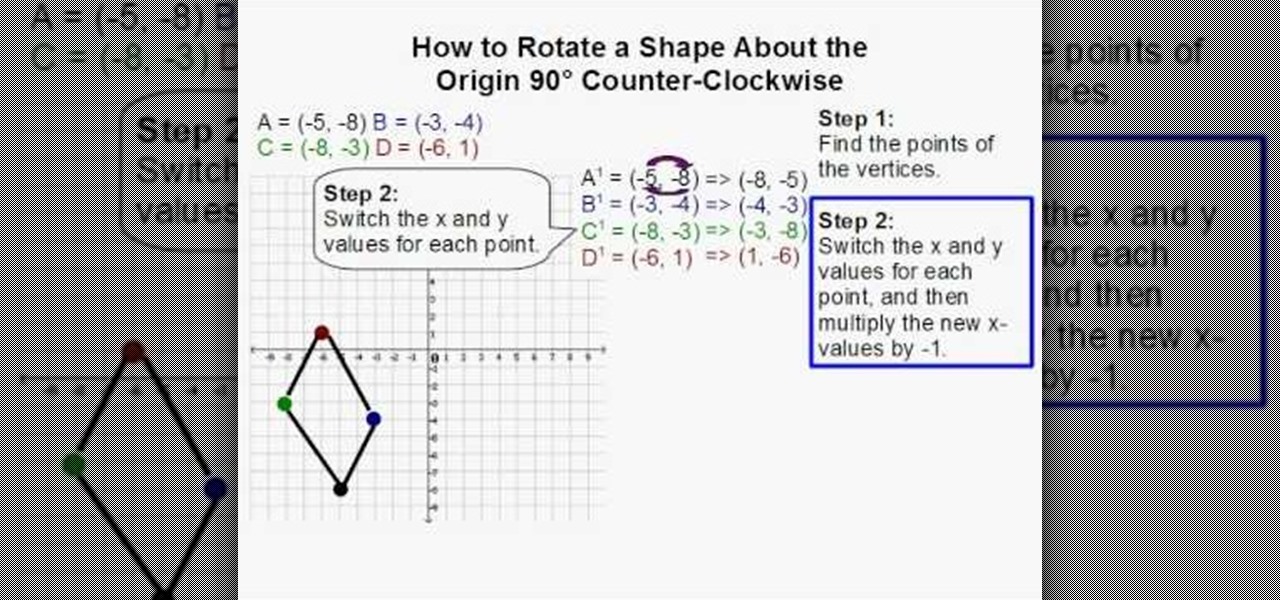
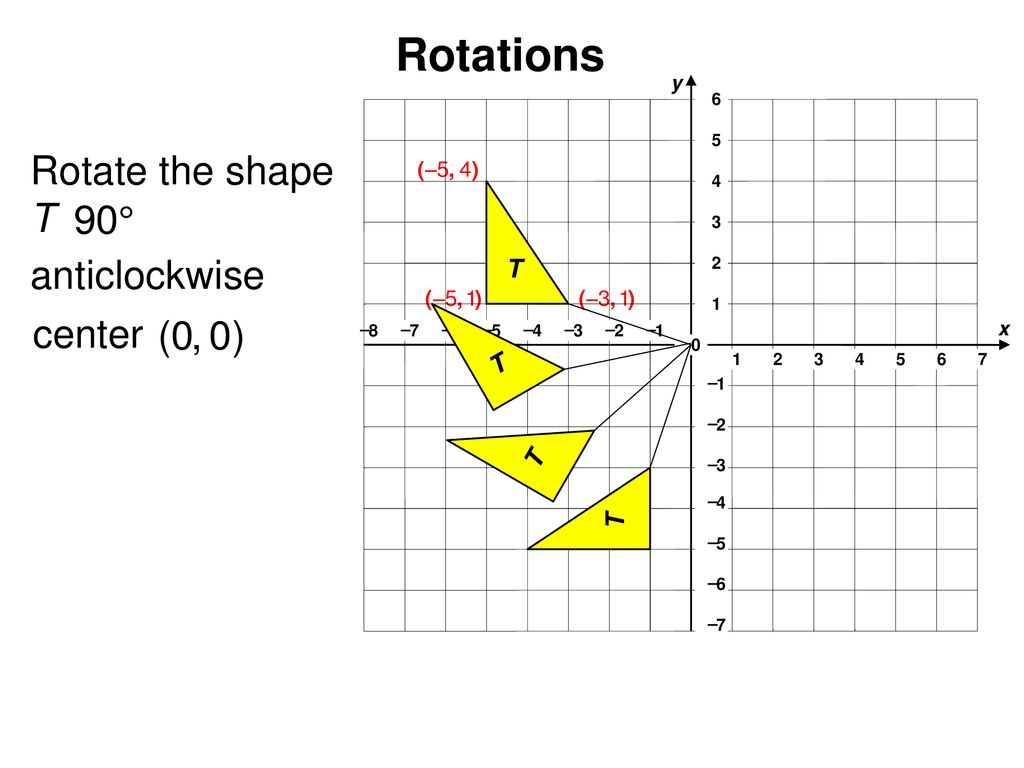
Proving trigonometric identities worksheet Special line segments in triangles worksheet Sum of the angles in a triangle is 180 degree worksheet Sum and product of the roots of a quadratic equationsĬomplementary and supplementary worksheetĬomplementary and supplementary word problems worksheet Nature of the roots of a quadratic equations Solving quadratic equations by completing square Solving quadratic equations by quadratic formula Solving linear equations using cross multiplication method Solving linear equations using substitution method Solving linear equations using elimination method When plot these points on the graph paper, we will get the figure of the image (rotated figure). In the above problem, vertices of the image areħ.
When we apply the formula, we will get the following vertices of the image (rotated figure).Ħ. When we rotate the given figure about 90° clock wise, we have to apply the formulaĥ. When we plot these points on a graph paper, we will get the figure of the pre-image (original figure).Ĥ. In the above problem, the vertices of the pre-image areģ. First we have to plot the vertices of the pre-image.Ģ.
#COUNTER CLOCKWISE ROTATION FORMULA HOW TO#
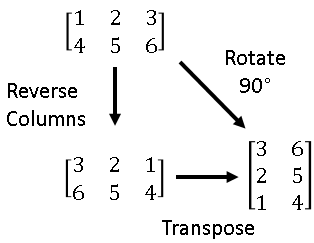
So the rule that we have to apply here is (x, y) -> (y, -x)īased on the rule given in step 1, we have to find the vertices of the reflected triangle A'B'C'Ī'(1, 2), B(4, -2) and C'(2, -4) How to sketch the rotated figure ?ġ. Here triangle is rotated about 90 ° clock wise. If this triangle is rotated about 90 ° clockwise, what will be the new vertices A', B' and C' ?įirst we have to know the correct rule that we have to apply in this problem. Let A ( -2, 1), B (2, 4) and C (4, 2) be the three vertices of a triangle. Let us consider the following example to have better understanding of reflection.
Here the rule we have applied is (x, y) -> (y, -x). Once students understand the rules which they have to apply for rotation transformation, they can easily make rotation transformation of a figure.įor example, if we are going to make rotation transformation of the point (5, 3) about 90 ° (clock wise rotation), after transformation, the point would be (3, -5).


 0 kommentar(er)
0 kommentar(er)
